Here be dragons

October 7, 2017

Medieval mapmakers noted the risk of an unknown kind by “here be dragons”. Attempts at measuring extreme risk should come with a similar warning. Just like the sailors of yesteryear, financial institutions will go into unknown territories and, just like the map makers of the earlier era, modern risk modellers have little to say.

The most difficult problem in measuring the risk is how to deal with very large and infrequent negative outcomes. Because these big losses don't happen very often, it is quite difficult to exploit historical observations to predict what sort of losses we might expect in the future. This is known as the fat tail problem.

Take the Standard & Poor’s 500 index. I have daily observations on the S&P-500 dating back to 1928 and the daily volatility of the S&P-500 is 1.1% Volatility only has a meaning under the normal distribution and it is straightforward to use a combination of the two to project any type of losses I want. If my portfolio is $1000, the ones in the millennium loss is $45. Not so shabby.

Expect, of course, it isn't like that. If I take my 88 year history of daily returns on the S&P 500, I find that the average annual worst loss is $47, not $26 as predicted by the normal. Over time these differences become bigger. The worst day over the past 88 years would give me the losses of $229 on 19 October 1987. Using volatility to measure risk would have lulled me into complacency.

I would have been eaten by a dragons.

This is summarised in the following figure which shows both the type of losses I would expect if I used the normal distribution and actually what happened.

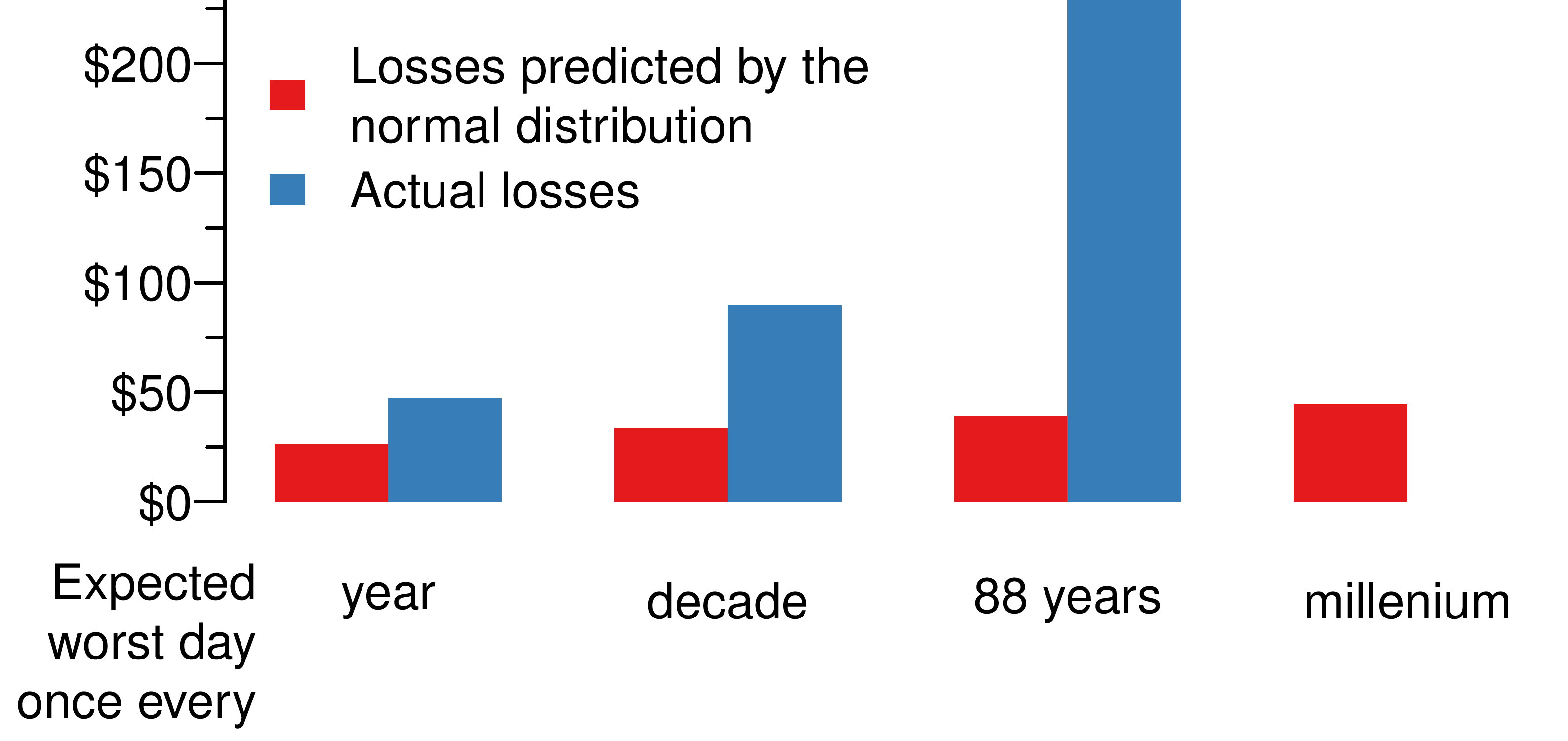
Volatility can only be an accurate measure of risk if and only if returns are normally distributed. And since they are not, volatility is an insufficient and can be a very misleading measure of risk. Often times it doesn't really matter all that much, the simplicity of volatility is all that we need in most cases.

If however we do care about the dragons, then be aware, they only bite us in times of stress. Volatility can not tell us anything about when that will happen.

Next time you hear someone use volatilities or standard deviations as measures of risk, especially extreme risk, remember that it is not so.

There is nothing new about this analysis, researchers have known about the fat tail problems for over 50 years, ever since the work of the future Nobel Prize winner Eugene Fama in 1963 and his PhD advisor Benoit B. Mandelbrot in the same year.

Still, even people and institutions that we would expect to know better can express surprising views on tail risk.

So if volatility and the normal distribution are not sufficient, what can we do? There are strategies, but none are easy. It requires better trained staff, faster computers, more time to create models, it is more expensive to hedge against tail risk and is harder to explain. So, it is about resources and communication and expectations. It is hard enough to talk about volatility in an accurate way to nonspecialists, any discussion of fat tails tends to go over the heads of most decision-makers.

There are two different avenues one can take. The first is based on understanding the deep nature of where risk is, how the people who work in the financial system interact and how they create risk. Use endogenous risk. Perhaps model the political risk.

If that is too complicated, we can just take a purely statistical approach, extreme value theory, or EVT. EVT is based on using the most extreme outcomes in a sample of observations of some object of interest to project the tail of the distribution of those objectives all the way to infinity.

As the next figure shows, we get much closer to what has been observed in history and the once in a millennium prediction is certainly much more realistic than the normal distribution predicts.

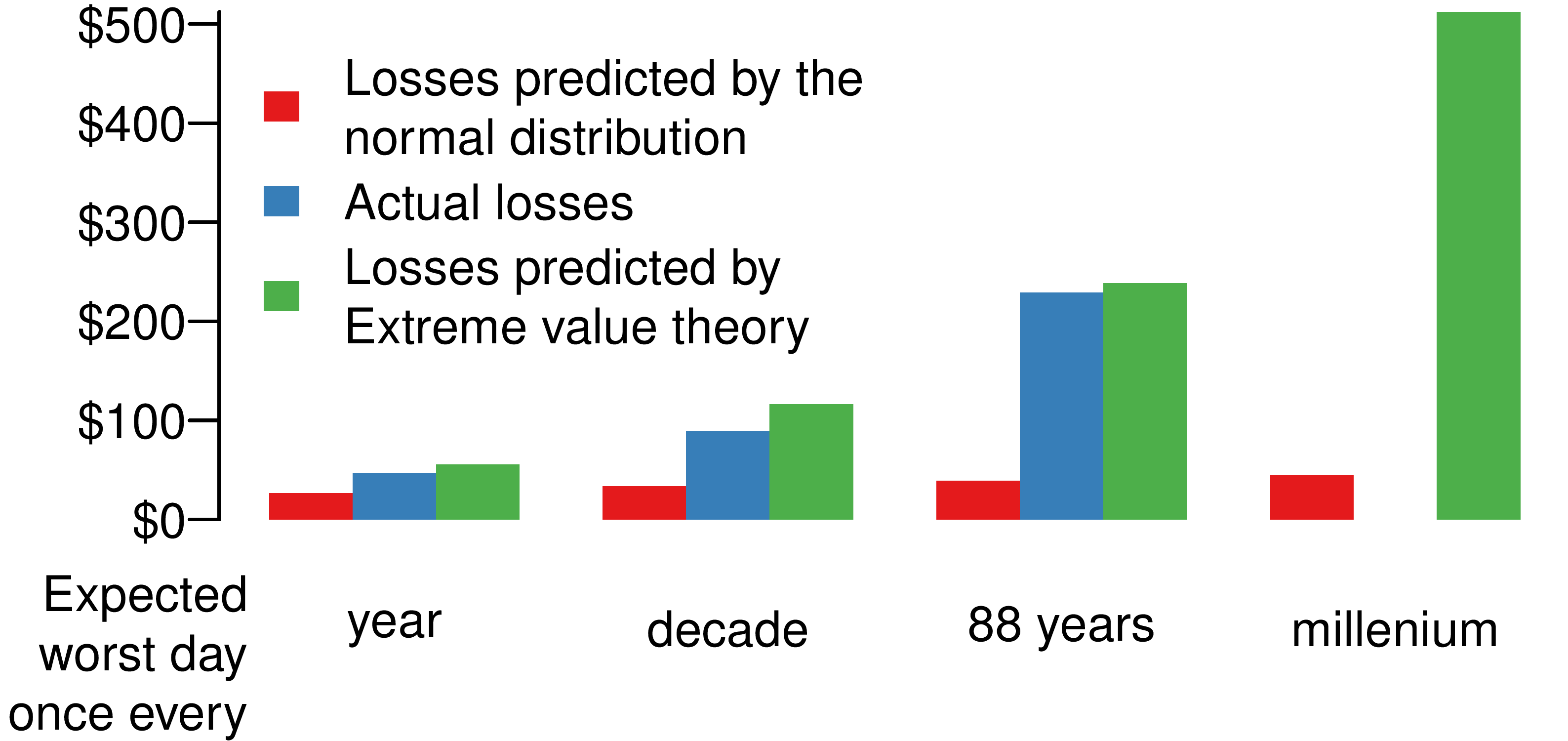
It isn't perfect, EVT depends on strong distributional assumptions likely to be violated in practice and it is difficult to find the right tuning parameters for the procedure. Still, it is the only game in town when it comes to using a purely statistical procedure to forecast extreme losses.

---

---